Suppose F Takes Nonnegative Values Show if F is Integrable Continuous at 0 and if F 0 0 Then
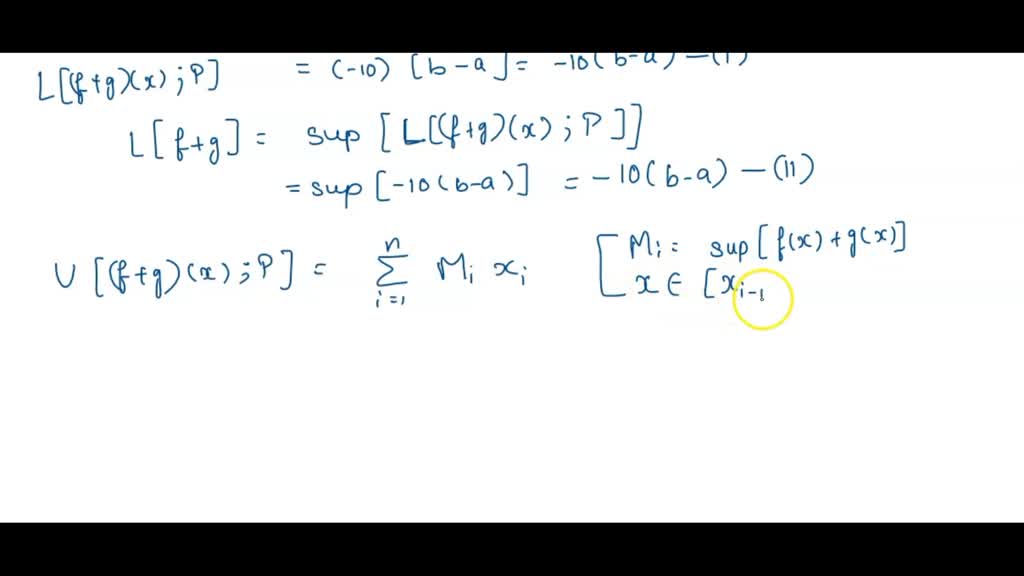
(1) Suppose that f [a,6] R is a monotonic functions; and g [a, 6] 1S either nonnegative integrable Or continuous function: Show that there is € € [a,6] such that f()g(c)dx f(a) g(z)dz + f (6) g(x)dx. (2) Show that <C1/n? +1) < 2 n=l Similarly show that i<2s for p > 1.

Related Question
Use the Darboux definition of the definite integral to provc: that f(r) + g(1) Is not integrable on [a,6]- Use thc Integrability €-Reformulation definition Theorem 2 of (hap tcr 13 of Suppl: Notes) to prOve that f(r) + g(r) is not integrablc [a,b].
Discussion
You must be signed in to discuss.
Video Transcript
find it in this problem which is given that he belongs to R and D is smaller than B. G. X. And effects are two functions that are given and we are required to prove that Fosco effects is not integral. Using Java's theorem and integrate ability and salary formulation theorem. So let us start with the solution in the first part we have to use the door box serum to prove that F plus G of X is not degradable. Firstly we need to find the F plus G of X effects is given. It will do when when X belongs to rational numbers and negative two when extras not belong to the national numbers then we have G X defined as two, then X belongs to set of rational numbers and negative eight. The next does not belong to set off racial numbers. Then the function F plus G. O fix a little bit defined as F plus G of X is equal to when X belongs to rational numbers. We have one plus two, that is three. So we did three. Then X belongs to set of rational numbers. Then we have When X does not belong to a set of rationing the best negative to negative eight, it becomes negative 10 said when X does not belongs to set of rational numbers. So this was the function F LSD affects no let I suppose that a partition of a B is done such that B is equal to maybe that's that B is equal to it's not is equal to a X men It is smaller than X two smaller than equal to and so on. Up to X and -1 is smaller than exit is equal to be. So this is the partition of a B. Now we will find the lower them off effortlessly topics for the party should be and it will be equal to summation of I is equal to one to end. Am I excited note that here am I represents the inference of am I is equal to information value of fx plus G X and it's belongs to XI -1 X I. So using these two values, the localism of the partition would be equal to informal value of F L s u of X is negative 10. So we have -10 which is the constant. We will take it out and in the summation we are left with Summation is equal to 1 to end. Dell off X I would be equal to X I minus x I minus one- XI -1. And that's what we equal to negative 10, multiplied by now taking the values of five from one to and we will get XI zero. Yes, X two -X men plus and so on. I do XN -X and -1 Xn minus. When note that in this bracket We have -10 and in this bracket all the values would get canceled except for exit and negative of X zero. So we have x and minus X zero left with us. And here minus 10 multiplied by this value X. N is equal to B. As shown in party shanty And zero is 8. So we have -10 multiplied by b minus A. So let it be the equation one which gives them lewis um of FLS geophysics for the partition B. Then lower some of F plus G would be equal to the supreme value of lowers them of FLS G of X. For the partition key eggs where the party should be that is equal to will be equal to supreme him off -10 multiplied by B -A. This will also be quilted -10, multiplied by B -A. This is the equation too. Now we will find the person for the f plus G. For partition p parties can be and it will be equal to summation of is equal to one to end. Am I excited? Where am I is the supreme um value of the function affects plus G. X. And x is equal to it belongs to x I minus 12 X I Are using these two values. We calculate this some and it will be equal to summation of Y is equal to one to end. What am I? We have three which is the supreme value of F plus G of X and four X. I. We have X I minus X. I -1 and this will be equal to three multiplied by for x. Science X. I minus. When we have the value as determined in part A. It will be equal to excited minus one. And this is conservation can be calculated in a similar manner as in part A. And it will be equal to b minus a. They have override three multiplied by b minus A. So this is the upper value of FLS G of X. For the partition P. Now that we have the uh person of FLS G. For the partition P. We can also find the person of F. Let's see and it will be equal to in film of a person of a flat G. Of X. For the partition P. And this will be equal to internal value of three multiplied by B -A. This will be equal to three, multiplied by B -A. Now this is the equation phone and we will use the equation to and full. So from equation two and four we get that the lower sum of F. L. S. D. Is not equal to the optimism of the function F plus G. And we know that according to the door box here. Um According to dropbox theorem, we have for the function F. It is integrated integrated ble if the liberalism of F is equal to a prism of F. So according to the double stadium, the function F plus G will not be integral. So we write that using double serum. The function F plus G of X is not integral. Doble. Gg rebel. Next we have to prove that this function is not interchangeable. Using Integra ability of silent reformulation theorem. So from the part A of this problem we have. The lure is um of Fosco affects what the party should be is equal to negatively and multiplied by b minus A. And a person of the function F L. S. D. Of X. For the partition P is equal to three, multiplied by B -A. Therefore we get that the difference of the uh person of the partition and the liberalism of the partition is equal to place your facts for the party should be. That's equal to three multiplied by B -A -10. multiplied by B -A. This is equal to 13 multiplied by b minus A. And we know that in the problem it is given that is smaller than B. This means that B -8 is a positive value which is greater than zero. This means that 13 multiplied by B -A is also greater than zero. And this value 13 multiplied by B is ready than some asylum where epsilon is a very small positive value. And therefore the difference of a person of FLS you effects for the partition P and blue prism of Fosco fix for the partition P is created. And or we can also say that it is not smaller than silent For some ε greater than zero. We know that F. S integral. Doble if and only if disagreeable if and only if the a person of F. First the party should be minus the lewisham of F. Four party should be is smaller than I am silent, but I Value of a silent which is greater than zero and a partition P in A B. Uh huh. Maybe. So you're using this theorem. We conclude that the function F plus G is not in the ribbon. So we write that using above theorem to get that F P S. G is not integrate, able and degradable. And this was the explanation. I hope you got the explanation. Thank you.
Source: https://www.numerade.com/ask/question/1-suppose-that-f-a6-r-is-a-monotonic-functions-and-g-a-6-1s-either-nonnegative-integrable-or-continuous-function-show-that-there-is-a6-such-that-fgcdx-fa-gzdz-f-6-gxdx-2-show-that-c1n-1-2-nl-15593/
0 Response to "Suppose F Takes Nonnegative Values Show if F is Integrable Continuous at 0 and if F 0 0 Then"
Post a Comment